2. Theorie
Um in der Hochfrequenztechnik zum korrekten
Messergebnis zu gelangen, bedarf es einiger Grundlagen zur drahtgebundenen
HF-Übertragung. In diesem Kapitel wird schrittweise und praxisnah erläutert
welche physikalischen Zusammenhänge hierbei zu beachten sind. Der Einfachheit
halber wird nur das Wechselspannungsverhalten von Koaxialkabeln untersucht.
Ohmsche Größen wie Längswiderstand und Isolationsleitwert werden nur am Rande
erwähnt.
Kabelersatzschaltbild
In Anlehnung an das Tiefpassfilter entstand dieses
Ersatzschaltbild in dem sich alle Leitungskonstanten wiederfinden. Die
Leitungskonstanten beziehen sich auf eine bestimmte Leitungslänge z.B. 1km. R’
ist der Widerstandsbelag in Ohm/km, er ergibt sich aus dem Leiterquerschnitt
und dessen Länge. L’ ist der Induktivitätsbelag in µH/km, weil jeder
stromdurchflossene Leiter ein Magnetfeld aufbaut welches Rückwirkungen auf die
Leitungsvorgänge hat. C’ ist der Kapazitätsbelag in nF/km und ergibt sich aus
dem Abstand der Leiter zueinander, dem Dielektrikum und der wirksamen
Oberfläche. G’ ist der Ableitungsbelag in µS/km, er hängt von der Qualität des
Dielektrikums ab.
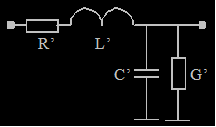
Moderne HF-Kabel haben dank ausgesuchter Materialien für
Leiter und Isolation geringe Verluste die erst Relevanz erlangen bei sehr
großen Kabellängen bzw. hoher zu übertragender Leistung.
Reales Kabel
In einem homogenen HF-Kabel lässt sich der kapazitive
Anteil nicht vom induktiven trennen.
Jeder noch so kurze Abschnitt enthält beide Elemente. Das
folgende Ersatzschaltbild zeigt ein praxisnahes Kabelmodell.
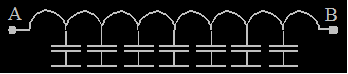
Anders als
bei einer diskret aufgebauten LC Kettenschaltung, bei der die Werte für die Schaltelemente
bekannt sind, besteht ein homogenes HF-Kabel aus einer unendlichen Anzahl
unendlich kleiner Kapazitäten und Induktivitäten die sich nicht einzeln
betrachten lassen. Dieser Aufbau ergibt für jedes einzelne Glied eine unendlich
hohe Übertragungsfrequenz.
Die Kapazitäts- und
Induktivitätsbeläge der Leitung lassen sich demnach nicht zur Berechnung der
oberen Grenzfrequenz heranziehen!
Wellenwiderstand, Kabelimpedanz Zk
Der Wellenwiderstand ist der Eingangswiderstand des
Kabels und ist das wichtigste Kriterium für die Anpassung. Er wird
herstellerseitig angegeben und ist abhängig von der Kabelgeometrie. Die
Kabellänge beeinflusst den Wellenwiderstand nicht. Koaxialkabel besitzen
Wellenwiderstände von 50 oder 75 Ohm.
Der Wellenwiderstand Zk
des RG58 Kabels beträgt ca. 50 Ohm.
(C’=100nF/km, L’=250µH/km)
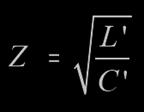
Dämpfung
Die Dämpfung eines HF-Kabels wird bestimmt durch die
Verlustwiderstände R’ und G’. Sie steigt mit der Länge des Kabels. Hinzu kommt
eine frequenzabhängige Dämpfung durch den Skineffekt, der den stromwirksamen
Leiterquerschnitt verringert und dadurch den Längswiderstand bei zunehmender
Betriebsfrequenz vergrößert. Das Koaxialkabel RG58 weist bei 1000MHz auf 100m
Länge eine Dämpfung von 60dB auf.
Um eine möglichst geringe Dämpfung bei hohen Frequenzen
zu erreichen sind die Kabellängen kurz zu halten.
Übertragungsbereich
Idealisiert ist der Übertragungsbereich einer angepassten
HF-Leitung frequenzlinear.
Bei steigender Frequenz entsteht durch den Skineffekt
allerdings ein Tiefpassverhalten.
Das Modell der LC-Kettenschaltung ist für die
Beschreibung der Frequenzlinearität nur eingeschränkt anwendbar. In der
LC-Kettenschaltung sind die Werte der Elemente vordefiniert und klar
voneinander getrennt. Anders bei der HF-Leitung. Ein Leiterstück kann beliebig
kurz sein und weist immer noch einen zur Länge proportionalen induktiven und
kapazitiven Anteil auf. Beliebig klein bedeutet aber auch dass die obere
Grenzfrequenz im Unendlichen liegt.
Anpassung
Professionelle HF-Netze sind angepasst. Das bedeutet,
dass Quellimpedanz, Leitungsimpedanz und Lastimpedanz identische Werte von z.B.
50 Ohm aufweisen. Dieses Verfahren hat den Vorteil, dass die Leitungslänge
nahezu vernachlässigbar wird und die eingespeiste Leistung verlustarm den
Verbraucher erreicht. Entlang der Leitung ist das Spannungsniveau konstant. Spannung
und Strom sind in Phase. Lediglich der ohmsche Widerstand der Leitung sowie der
Skineffekt begrenzen die Kabellänge.
Nur bei Anpassung wird die Leistung am Lastwiderstand
maximiert. Da im Kabel die induktiven und kapazitiven Blindwiderstände
überwiegen und der ohmsche Anteil vernachlässigbar ist, wird kaum Wirkleistung
über der Leitung umgesetzt.
Wellenwiderstandsmodell
Eine häufig gestellte Frage betrifft die Rolle der
Kabelimpedanz bei der Anpassung. Zur Erklärung soll das Wellenwiderstandsmodell
dienen:
Masche I stellt die Einspeisung der Energie in das
Kabel-, Masche II die Entnahme der
Energie durch den Lastwiderstand dar. Die beiden Prozesse finden nicht
zeitgleich statt sondern durch die Laufzeit des Signals im Kabel verzögert:
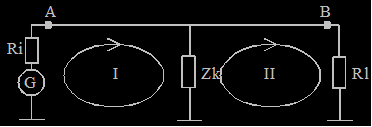
Das Kabel schließt mit
seinem Wellenwiderstand die HF-Quelle ab und ist Zwischenspeicher der zu
übertragenden Energie. Der Lastwiderstand wiederum schließt das Kabel ab.
In der HF-Leitung überwiegen kapazitive und induktive
Blindwiderstände. Die Leitung verbraucht
keine Energie sondern speichert sie bis zum Erreichen des Lastwiderstandes in
ihren elektrischen und magnetischen Feldern.
Bei Anpassung sind die Impedanzen Ri
= Zk = Rl. Spannung und Strom sind an jeder Stelle in
Phase, die übertragbare Energie erreicht ihr Maximum.
Bei Abweichung der Impedanzen (Fehlanpassung) entstehen
Phasenverschiebungen und die von der Leitung aufnehmbare und übertragbare
Energie verringert sich.
Durch Laufzeiten
im HF-Kabel ist der Augenblick der Einspeisung des Signals am Kabelanfang nicht
identisch mit dem Moment der Abgabe an den Verbraucher.
Bei der Leitung von
Hochfrequenz überlagern sich drei physikalische Vorgänge:
die endliche
Geschwindigkeit von elektrischen Signalen in Leitern, der Wellencharakter von
Hochfrequenz und der komplexe Wellenwiderstand des Kabels.
Laufzeit vs. Frequenz
Reflexionen
und stehende Wellen sind von Bedeutung, wenn die Kabellänge groß verglichen mit
der Signal-Wellenlänge ist.
Stehende Wellen
Wenn bei
Fehlanpassung z.B. die Kabelimpedanz von der Quellimpedanz abweicht (Zk≠Ri), kann das Kabel nicht
die gesamte HF-Energie übertragen. In diesem Falle weicht die Spannung über der
Last von der der Quelle ab. Die nicht aufgenommene Energie beginnt sich
auszubreiten und fließt zur Quelle zurück um dort in Wärme umgesetzt zu werden.
Die
zurücklaufende Welle bildet mit der hinlaufenden Interferenzen bzw. stehende
Wellen entlang der Leitung aus.
Ursache hierfür sind Reflexionen der Hochfrequenz in der
Leitung. Der Rückfluss erfolgt mit einem Phasenwinkel von +90° bis –90°
abhängig von der Art der Fehlanpassung.
Neben den Verlusten durch Fehlanpassung besteht bei
Sendeendstufen zusätzlich die Gefahr der Überlastung. Zur Veranschaulichung der Ursachen stehender
Wellen dient das Modell der L-C-Kettenschaltung. Die folgenden zwei Beispiele
dienen zur Extremwertbetrachtung:
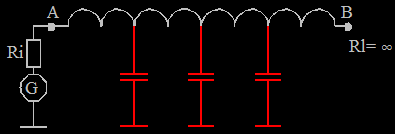
Lastimpedanz >>
Leitungsimpedanz (Leerlauf)
Hierzu wird der Lastwiderstand entfernt. Bei offenem
Ausgang des Kabels B entsteht dort Spannungsmaximum und Stromminimum,
es dominiert der kapazitive Anteil der Leitung. Kapazitäten sind Blindlasten
und geben die aufgenommene Energie mit einem negativen Phasenwinkel wieder ab,
sie reflektieren die Hochfrequenz. Im Abstand von λ/4 vom Leitungsende bildet sich ein
Spannungsminimum aus. Es herrscht Totalreflexion, die gesamte HF-Energie wird
zum Anschluss A reflektiert und am Generator-Innenwiderstand in Wärme
umgewandelt.
Am Anschluss B wird keine Leistung umgesetzt weil der
Laststrom null ist.
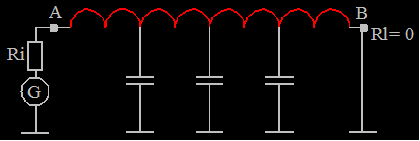
Lastimpedanz <<
Leitungsimpedanz (Kurzschluss)
Hierzu wird anstelle des Lastwiderstandes B ein
Kurzschluss eingefügt. Bei kurzgeschlossenem Ausgang entsteht dort Strommaximum
und Spannungsminimum, es dominiert der induktive Anteil der Leitung.
Induktivitäten sind Blindlasten und geben die aufgenommene Energie mit einem
positiven Phasenwinkel wieder ab, sie reflektieren die Hochfrequenz. Im Abstand
von λ/4 bildet sich ein Spannungsmaximum
aus. Es herrscht Totalreflexion, die gesamte HF-Energie wird zum Anschluss A
reflektiert und am Generator-Innenwiderstand in Wärme umgewandelt. Am Anschluss
B wird keine Leistung umgesetzt weil die Spannung null ist.
Urheberrechtsbelehrung
Die Verwendung dieses Dokuments (auch
auszugweise) in Publikationen jeder Art
darf nur mit Quellenangabe erfolgen. ©
2019 www.elektronenlabor.de